Depression has been the largest mental health problem affecting the public health. Early detection of persons suffering from depression is crucial for effective mitigation and treatment. The key to this can only be achieved when clear symptoms of depression are used to detect patients’ depression conditions. The objective of this study is to develop a predictive model for depression that uses the symptoms. The study used both simulated data and real data from the hospitals. The study developed hidden markov model that help to compute the transitional probabilities. The study also used the logistic regression to assess the predictive power of the symptoms of depression. The study found that insomnia positively influence the probability of depression among the patients. The study also found that guilt positively influence the probability of depression among the patients. From the results, the study found that suicidal positively influence the probability of depression among the patients and also fatigue influence the probability of depression. From the study it was also found that retardation positively influence the probability of depression. Finally, found that the change in anxiety negatively influence the probability of depression among the patients. The study also conclude that the predictive model can be used to predict the depression status of the patients by a medical doctor given that the observable symptoms are present.
| Published in | American Journal of Theoretical and Applied Statistics (Volume 14, Issue 1) |
| DOI | 10.11648/j.ajtas.20251401.11 |
| Page(s) | 1-11 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Depression, Transition Probability, Hidden Markov, Logistic
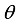 is the vector of the parameters describing the model, all the required inference will be based on the posterior distribution of
is the vector of the parameters describing the model, all the required inference will be based on the posterior distribution of 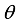 . Given the data set y, from the Bayes' theorem:
. Given the data set y, from the Bayes' theorem: 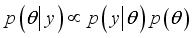
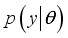 is the likelihood and
is the likelihood and 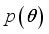 is the prior distribution of the parameters. Depending on the choice of the loss function, inference about the parameter
is the prior distribution of the parameters. Depending on the choice of the loss function, inference about the parameter 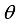 is based on the posterior distribution. For instance if the squared loss function is used then the posterior mean is the estimator for the parameter
is based on the posterior distribution. For instance if the squared loss function is used then the posterior mean is the estimator for the parameter 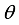 . i.e
. i.e 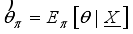 .
. 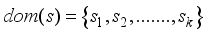 , such that each
, such that each 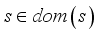 is called a latent (or hidden) state. We denote by
is called a latent (or hidden) state. We denote by  the set of observable variables, such that the ith observation
the set of observable variables, such that the ith observation 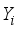 takes values on some set
takes values on some set 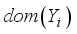 . In medical domains, each
. In medical domains, each 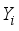 will often refer to measured data such as symptoms, while the latent variable S will refer to some state of the underlying disease (i.e disease remitting mental wellbeing). The disease process of interest is assumed discrete over the time points
will often refer to measured data such as symptoms, while the latent variable S will refer to some state of the underlying disease (i.e disease remitting mental wellbeing). The disease process of interest is assumed discrete over the time points  , where the value of the latent variable and the observables that hold at time t will be denoted by
, where the value of the latent variable and the observables that hold at time t will be denoted by 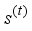 and
and 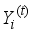 respectively. The hidden Markov model comprises of the bivariate discrete time process of the form
respectively. The hidden Markov model comprises of the bivariate discrete time process of the form 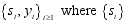 consist of unobservable Markov chain states and conditional on
consist of unobservable Markov chain states and conditional on 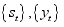 being sequence of random variables that are independent and that conditional distribution of
being sequence of random variables that are independent and that conditional distribution of 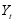 only depend on
only depend on 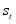 . Sequence
. Sequence 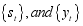 are referred to as the state and observed sequences respectively
are referred to as the state and observed sequences respectively 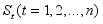 which assume on the m values in the transitional matrix
which assume on the m values in the transitional matrix 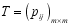 and probability of being in the first state or the initial probability distribution
and probability of being in the first state or the initial probability distribution 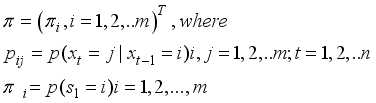
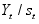 has a parametric form
has a parametric form 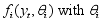 being a vector consisting of unknown parameters. In fitting the hidden markov chain model the parameters will be estimated including both the transitional, initial probabilities and the probability distribution parameters. The transitional matric in the hidden state is a square matrix in which each probabilities in the row is modelled using the ordered probit logit model. In estimation of the distribution parameters, the study can use Bayesian method with the assumption that the parameters of the distribution follows a distribution called the prior distribution. The hidden markov chain models have been used by many research in modeling real life phenomenon. Hidden Markov models (HMM) can be seen as an extension of Markov models to the case where the observation is a probabilistic function of the state, i.e. the resulting model is a doubly embedded stochastic process, which is not necessarily observable, but can be observed through another set of stochastic processes that produce the sequence of observations. Let
being a vector consisting of unknown parameters. In fitting the hidden markov chain model the parameters will be estimated including both the transitional, initial probabilities and the probability distribution parameters. The transitional matric in the hidden state is a square matrix in which each probabilities in the row is modelled using the ordered probit logit model. In estimation of the distribution parameters, the study can use Bayesian method with the assumption that the parameters of the distribution follows a distribution called the prior distribution. The hidden markov chain models have been used by many research in modeling real life phenomenon. Hidden Markov models (HMM) can be seen as an extension of Markov models to the case where the observation is a probabilistic function of the state, i.e. the resulting model is a doubly embedded stochastic process, which is not necessarily observable, but can be observed through another set of stochastic processes that produce the sequence of observations. Let 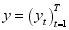 be the vector of observed variables, indexed by time. HMMs assume that the distribution of each observed data point
be the vector of observed variables, indexed by time. HMMs assume that the distribution of each observed data point 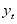 depends on an unobserved (hidden) variable, denoted
depends on an unobserved (hidden) variable, denoted 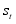 , that takes on values from 1 to k. The hidden variable
, that takes on values from 1 to k. The hidden variable 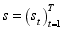 characterizes the “state" in which the generating process is at any time t. HMMs further postulate a Markov Chain for the evolution of the unobserved state variable and, hence, the process for
characterizes the “state" in which the generating process is at any time t. HMMs further postulate a Markov Chain for the evolution of the unobserved state variable and, hence, the process for 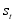 is assumed to depend on the past realizations of
is assumed to depend on the past realizations of 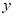 and
and 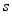 only through
only through 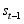 :
: 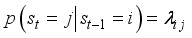
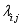 is the generic element of the transition matrix
is the generic element of the transition matrix 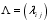
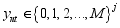 where the j symptoms scores reported by individual
where the j symptoms scores reported by individual 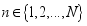 on event t, where for our study J=6 and M=2; we use generalized notation because the basic modelling strategy may be applied to other types of related. The study assume that at any given time, any individual is either in a depressed state D or in a Normal state N. the study assume that a person in state N does not show symptom of depression. The study also indicate that a person in state D exhibit the symptoms of depression. This study used a logistic model to link the observed symptoms J to the latent state.
on event t, where for our study J=6 and M=2; we use generalized notation because the basic modelling strategy may be applied to other types of related. The study assume that at any given time, any individual is either in a depressed state D or in a Normal state N. the study assume that a person in state N does not show symptom of depression. The study also indicate that a person in state D exhibit the symptoms of depression. This study used a logistic model to link the observed symptoms J to the latent state. 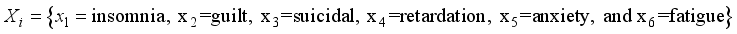
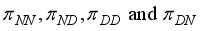 are functions of the
are functions of the 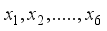 . Simply written as
. Simply written as 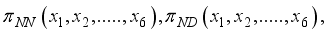
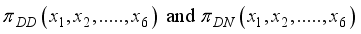 , without loss of generality simply write as
, without loss of generality simply write as 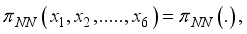
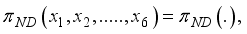
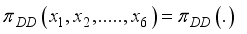
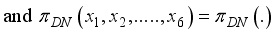 now if atleast on of the
now if atleast on of the 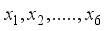 is greater than 0, then
is greater than 0, then 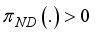 if at least one of the
if at least one of the 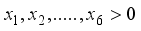 or
or 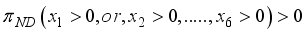
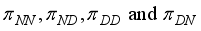 are transitional probabilities which they form a
are transitional probabilities which they form a 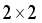 transitional matrix
transitional matrix 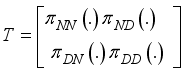
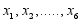 to guide the as this state of the police officer. Suppose that the state of the police officer us N-no depression and D-depressed as presented in Figure 2, this is a binary output.
to guide the as this state of the police officer. Suppose that the state of the police officer us N-no depression and D-depressed as presented in Figure 2, this is a binary output. 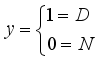 asthis binary results
asthis binary results 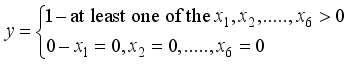
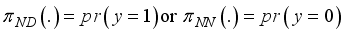
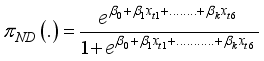 (1)
(1) 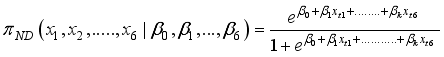 (2)
(2) 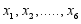 to predict the y’s. Y’s are the hidden state where as X’s are the observed state. The probability of the hidden state
to predict the y’s. Y’s are the hidden state where as X’s are the observed state. The probability of the hidden state 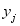 given the observable states X’s for a police officer j, j=1, 2, 3,…., n is given by
given the observable states X’s for a police officer j, j=1, 2, 3,…., n is given by 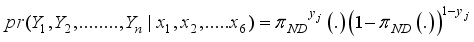 (3)
(3) 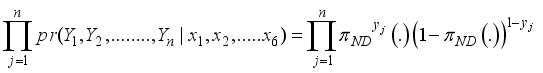
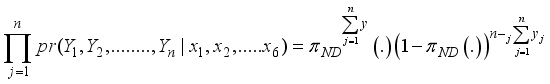 (4)
(4) 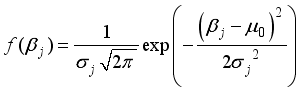 (5)
(5) 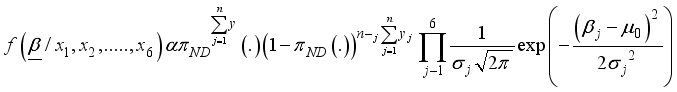 (6)
(6)  represent a vector of the logistic regression parameters to be estimated, and using the Bayesian method, the information about the parameters
represent a vector of the logistic regression parameters to be estimated, and using the Bayesian method, the information about the parameters 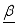 can only be found from posterior distribution
can only be found from posterior distribution 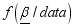 This study used the Gibbs sampler algorithm to produce the estimate of the parameters
This study used the Gibbs sampler algorithm to produce the estimate of the parameters 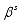 from the previous estimate
from the previous estimate 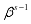 using the following steps
using the following steps 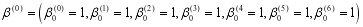
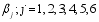 is updated as follows
is updated as follows 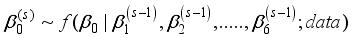
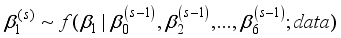
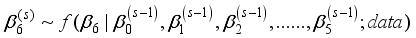
coefficient | mean | standard deviation | naïve error |
|---|---|---|---|
beta0 | -0.03484 | 0.0301 | 0.0006731 |
beta1 | 0.24144 | 0.02628 | 0.0005875 |
beta2 | 0.23969 | 0.02691 | 0.0006017 |
beta3 | 0.23525 | 0.02739 | 0.0006125 |
beta4 | 0.23863 | 0.02868 | 0.0006413 |
beta5 | 0.23662 | 0.02669 | 0.0005967 |
beta6 | 0.25061 | 0.02866 | 0.0006409 |

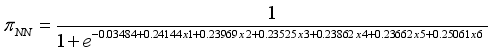
Y | insomnia | guilt | suicidal | retardation | anxiety | fatigue | prob |
|---|---|---|---|---|---|---|---|
1 | 3 | 1 | 3 | 2 | 0 | 3 | 0.946156 |
1 | 2 | 3 | 3 | 3 | 2 | 0 | 0.955395 |
1 | 0 | 3 | 2 | 1 | 3 | 3 | 0.945698 |
1 | 0 | 0 | 0 | 1 | 3 | 2 | 0.804895 |
1 | 3 | 2 | 0 | 2 | 0 | 0 | 0.838676 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.500136 |
1 | 1 | 3 | 2 | 0 | 2 | 1 | 0.893054 |
1 | 0 | 1 | 0 | 1 | 3 | 1 | 0.803173 |
1 | 0 | 2 | 0 | 0 | 3 | 3 | 0.870855 |
1 | 0 | 3 | 1 | 3 | 2 | 3 | 0.945974 |
| [1] | Bi B., Xiao X., Zhang H., Gao J., Tao M., Niu H., et al. (2012). A comparison of the clinical characteristics of women with recurrent major depression with and without suicidal symptomatology. Psychol. Med. 42, 2591–2598 10.1017. |
| [2] | Bryan C. J., Morrow C. E., Etienne N., Ray Sannerud B. (2013). Guilt, shame, and suicidal ideation in a military outpatient clinical sample. Depress. Anxiety 30, 55–60 |
| [3] | Elliott R., Lythe K., Lee R., Mckie S., Juhasz G., Thomas E. J., et al. (2012). Reduced medial prefrontal responses to social interaction images in remitted depression. Arch. Gen. Psychiatry 69, 37. |
| [4] | Fried, 2015 E. I. FriedProblematic assumptions have slowed down depression research: why symptoms, not syndromes are the way forward Front. Psychol., 6 (MAR) (2015), p. 309 |
| [5] | Grahek, J. Everaert, R. M. Krebs, E. H. W. Koster (2018). Cognitive control in depression: toward clinical models informed by cognitive neuroscience Clin. Psychol. Sci., 6(4), pp. 464-480. |
| [6] | Lallukka T, Podlipskytė A, Sivertsen B, Andruškienė J, Varoneckas G, Lahelma E, Ursin R, Tell GS, Rahkonen O. 2016. Insomnia symptoms and mortality: a register-linked study among women and men from Finland, Norway and Lithuania. J Sleep Res. 25(1): 96–103. |
| [7] | Morin CM, Benca R. 2012. Chronic Insomnia. The Lancet 379(9821): 1129–1141. |
| [8] | Morin, C. M., Belleville, G., Bélanger, L., & Ivers, H. (2011). The Insomnia Severity Index: psychometric indicators to detect insomnia cases and evaluate treatment response. Sleep, 34(5), 601–608. |
| [9] | Oskooyee KS, Rahmani AM, Kashani MMR (2011) Predicting the severity of major depression disorder with the Markov chain model. Int. Conf Biosci Biochem Bioinforma Singap 5: 30–34. |
| [10] | Pallesen S, Sivertsen B, Nordhus IH, Bjorvatn B. 2014. A 10-year trend of Insomnia prevalence in the adult Norwegian population. Sleep Med. 15(2): 173–179. |
| [11] | Parthasarathy S, Vasquez MM, Halonen M, Bootzin R, Quan SF, Martinez FD, Guerra S. 2015. Persistent Insomnia is associated with mortality risk. Am J Med. 128(3): 268–275. |
| [12] | O. Cappe, E. Moulines, and T. Ryden, Inference in Hidden Markov Models (Springer, New York, 2005), pp. 1–650 |
| [13] |
Mars B, Heron J, Crane C, Hawton K, Kidger J, Lewis G, Macleod J, Tilling K, Gunnell D. Differences in risk factors for self-harm with and without suicidal intent: findings from the ALSPAC cohort. J Affect Disord. 2014 Oct; 168: 407-14.
https://doi.org/10.1016/j.jad.2014.07.009 Epub 2014 Jul 17. |
| [14] | Long, K. M., & Meadows, G. N. (2018). Simulation modelling in mental health: A systematic review. Journal of Simulation, 12(1),76-85. |
APA Style
Mwangi, C., Nyongesa, K., Odero, E. A. (2025). Predictive Model for Depression Without Medical Intervention. American Journal of Theoretical and Applied Statistics, 14(1), 1-11. https://doi.org/10.11648/j.ajtas.20251401.11
ACS Style
Mwangi, C.; Nyongesa, K.; Odero, E. A. Predictive Model for Depression Without Medical Intervention. Am. J. Theor. Appl. Stat. 2025, 14(1), 1-11. doi: 10.11648/j.ajtas.20251401.11
@article{10.11648/j.ajtas.20251401.11,
author = {Charles Mwangi and Kennedy Nyongesa and Everlyne Akoth Odero},
title = {Predictive Model for Depression Without Medical Intervention},
journal = {American Journal of Theoretical and Applied Statistics},
volume = {14},
number = {1},
pages = {1-11},
doi = {10.11648/j.ajtas.20251401.11},
url = {https://doi.org/10.11648/j.ajtas.20251401.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajtas.20251401.11},
abstract = {Depression has been the largest mental health problem affecting the public health. Early detection of persons suffering from depression is crucial for effective mitigation and treatment. The key to this can only be achieved when clear symptoms of depression are used to detect patients’ depression conditions. The objective of this study is to develop a predictive model for depression that uses the symptoms. The study used both simulated data and real data from the hospitals. The study developed hidden markov model that help to compute the transitional probabilities. The study also used the logistic regression to assess the predictive power of the symptoms of depression. The study found that insomnia positively influence the probability of depression among the patients. The study also found that guilt positively influence the probability of depression among the patients. From the results, the study found that suicidal positively influence the probability of depression among the patients and also fatigue influence the probability of depression. From the study it was also found that retardation positively influence the probability of depression. Finally, found that the change in anxiety negatively influence the probability of depression among the patients. The study also conclude that the predictive model can be used to predict the depression status of the patients by a medical doctor given that the observable symptoms are present.},
year = {2025}
}
TY - JOUR T1 - Predictive Model for Depression Without Medical Intervention AU - Charles Mwangi AU - Kennedy Nyongesa AU - Everlyne Akoth Odero Y1 - 2025/01/07 PY - 2025 N1 - https://doi.org/10.11648/j.ajtas.20251401.11 DO - 10.11648/j.ajtas.20251401.11 T2 - American Journal of Theoretical and Applied Statistics JF - American Journal of Theoretical and Applied Statistics JO - American Journal of Theoretical and Applied Statistics SP - 1 EP - 11 PB - Science Publishing Group SN - 2326-9006 UR - https://doi.org/10.11648/j.ajtas.20251401.11 AB - Depression has been the largest mental health problem affecting the public health. Early detection of persons suffering from depression is crucial for effective mitigation and treatment. The key to this can only be achieved when clear symptoms of depression are used to detect patients’ depression conditions. The objective of this study is to develop a predictive model for depression that uses the symptoms. The study used both simulated data and real data from the hospitals. The study developed hidden markov model that help to compute the transitional probabilities. The study also used the logistic regression to assess the predictive power of the symptoms of depression. The study found that insomnia positively influence the probability of depression among the patients. The study also found that guilt positively influence the probability of depression among the patients. From the results, the study found that suicidal positively influence the probability of depression among the patients and also fatigue influence the probability of depression. From the study it was also found that retardation positively influence the probability of depression. Finally, found that the change in anxiety negatively influence the probability of depression among the patients. The study also conclude that the predictive model can be used to predict the depression status of the patients by a medical doctor given that the observable symptoms are present. VL - 14 IS - 1 ER -